比较构造法在行测计算问题中的应用
行测运算题必须采用一定技巧才能提高解题效率,小编在此为大家推荐比较构造法,希望能给各位考生带来帮助。
一、什么是比较构造法
对同一事物有两种或两种以上不同方案的描述,通过比较方案间的异同建立联系,构造关系式,这种方法就是比较构造法。与普通的方程法相比,比较构造法更为便捷,节约了做题时间,从而提高做题速度。
二、典型常见题型分析
【例】若干学生住若干房间,如果每间住4人,则有20人没地方住,如果每间房住8人,则有一间房只有4人住,那么共有多少间房?
【解析】
方法一:可以通过学生总人数不变来列等量关系式,设房间数为x,那么我们可以建立的等量关系式为4x+20=8(x-1)+4,求得x=6,则共有6间房。
方法二:已知简单的两种方案,列出方案

通过表格可知,方案二相比方案一可以多住4-(-20)=24人,那为什么同样数量的房间方案二要多住这么多呢?其实主要是由于每间房住的人数不同,方案二每间房要比方案一多住8-4=4人。所以方案二相较于方案一,总共多住24人,每间房多住4人,那么房间数所求为24÷4=6间房。所以我们有时候并不需要通过设未知数和列方程来进行解题,只要比较两种方案之间的差别也可以快速解决这类题目。
【练一练】某工程队计划在某一时间内修一条路。若每天修200米,则还剩下1000米;若每天修250米,则可多修200米。这条路的工作时间是()天。
【解析】
已知方案及比例关系列出方案
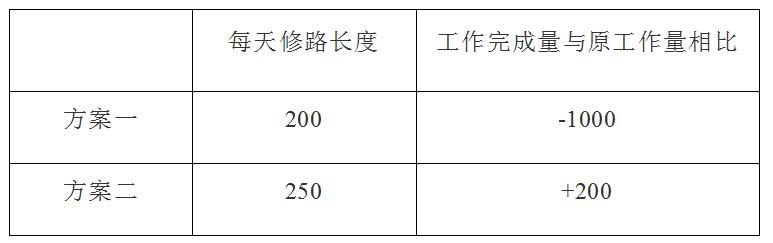
比较差异构造关系式,两种方案下每天的工作量相差50米,剩余量相差1200米,故修了1200÷50=24天。
对同一事件有两种或两种以上的不同方案,比较方案之间的异同,建立方案之间的联系,构造关系式,解出答案。因此,比较构造法的一般步骤:
1、列出方案;
2、比较方案之间的差别与联系;
3、构造关系式;
4、求解。
各位小伙伴们,之后也要多找一些这样的题目练习,巩固知识,加深对比较构造法的理解和使用,在考场上灵活应对!