行测数量关系排列组合之隔板模型
在行测数量关系中排列组合问题是一个高频的考点，排列组合同时也是很多考生的难点，但在排列组合中有一类把相同元素分给不同对象的题目，这类题目题型特征明确，且有固定的解题思路，这就是今天小编带大家学习的排列组合问题中的隔板模型。下面结合几道例题带大家来认识下隔板模型：
一、隔板模型的题型特征
将n个相同元素分给m个不同的对象，每个对象至少有1个。(所要分的元素必须完全相同，所要分的元素必须分完，绝不允许有剩余;每个对象至少分到1个，决不允许出现分不到元素的对象。)
二、例题
1.某城市一条道路上有4个十字路口，每个十字路口至少有1名交通协管员，现将8个协管员名额分配到这4个路口，则每个路口协管员名额的分配方案有多少种?
A.35 B.70 C.96 D.114
【答案】A。解析：题干要求将8个协管员名额分配在4个不同的十字路口，每个路口至少一个(注意这里是分配相同元素，都是协管员)，我们可以将此事理解为将8个相同的元素分成4堆，每堆至少1个。可考虑如下分法，○○∣○○∣○∣○○○或者○∣○○○○∣○○∣○等等，其实想要把8个相同元素分成4堆，只需在这8个元素形成的空位中选出3个，放上3块隔板即可。但需注意，因为每堆至少有一个元素，故隔板不可放置在两端，只能放在中间7个空位中且每个空位只能放置一块板，也就是从7个空位中选择3个空位放置3块板即可。此外，任意两块隔板改变顺序对结果无影响(比如，3个相同的球分两堆，则等同于两个空放1块隔板，则结果为2个球和1个球;1球和2个球，实际是一样的)故为组合问题。结果
,所以此题择A。
,所以此题择A。 2.2022年高考强基计划中北京大学给了我校10个推荐名额,现准备将这10个推荐名额分配给高三理科的3个班级,这3个班级每班至少要给2个名额,则关于分配方案有多少种?
A.46 B.20 C.15 D.13
【答案】C。解析：题干中出现了“将10个推荐名额分给3个班级”所以此题可用为隔板模型。但题干中问的是每个班级至少分2个，而标准模型是每个对象至少分1个，所以这里每个班级都是多分了一个，则可以先给每个班级各分一个，此时剩10-3=7个，此题就变成了把7个对象分给3个班级，每个班级至少分1个。只需在这7个元素形成的空位中选出2个，放上2块隔板即可。此外，任意两块隔板改变顺序对结果无影响故为组合问题。结果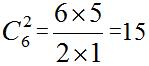
,所以此题选C。
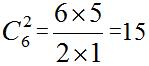,所以此题选C。 3.某班级买了6个相同的足球发放给3个班级。问一共有多少种不同的发放方法有多少种?
A.27 B.28 C.30 D.32
【答案】B。解析：此题没有提到每个班级至少1个，但可以通过转化使之满足。即先从每个班级借1个足球，此时共有6+3=9个，有借必有还，相当于这9个分给3个班级且每个班级至少分1个。只需在这9个元素形成的8个空位中选出2个，放上2块隔板即可。此外，任意两块隔板改变顺序对结果无影响故为组合问题。结果
，所以此题选B。
，所以此题选B。 隔板模型是考试中的常考题型之一，有很强的规律性，要熟练掌握解题方法，准确巧妙地识别题型特点和采用做题技巧，以便提高做题效率。
