行测数量关系以“定理”定思路——平面几何求面积
几何问题是行测数量关系中的高频题型,可以分为平面几何和立体几何两类,主要考查跟几何图形相关的基本公式和性质等。其中平面几何的题目常常涉及到利用基本公式求各区域的面积,有些同学不擅长用基本公式解题,看到题目毫无思路。那么大家可以记一些常用的定理,遇到平面几何求面积时不再望而却步。今天小编带领大家学习两个定理“蝴蝶定理”和“风筝定理”。
一、蝴蝶&风筝
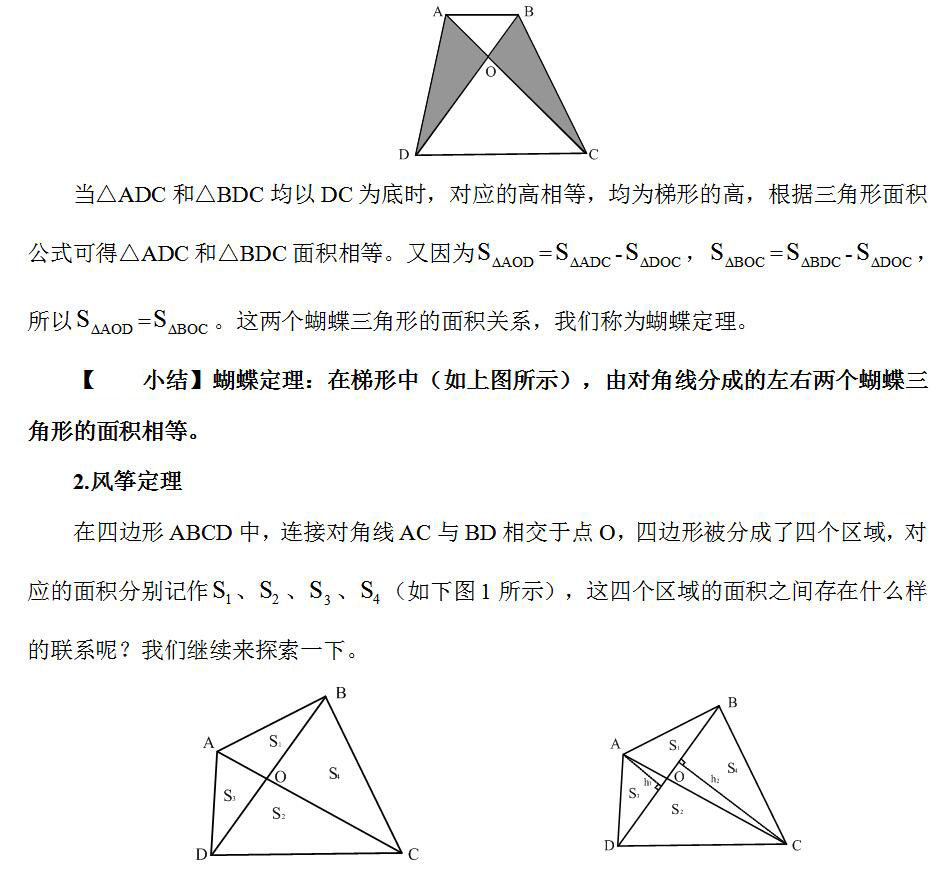
1.蝴蝶定理
在梯形ABCD中,AB∥CD,连接对角线AC和BD交于点O,将梯形分成了四个区域,其中△AOD和△BOC看起来像蝴蝶的一对翅膀,所以我们称这两个三角形为蝴蝶三角形(如下图阴影部分所示),这两个蝴蝶三角形的面积有什么关系呢?我们一起来看一下:

二、实战操作
一块种植花卉的矩形土地如图所示,AD是AB的2倍,E是CD的中点,甲、乙、丙、丁、戊区域分别种植白花、红花、黄花、紫花、白花。问种植白花的面积占矩形土地的面积的:
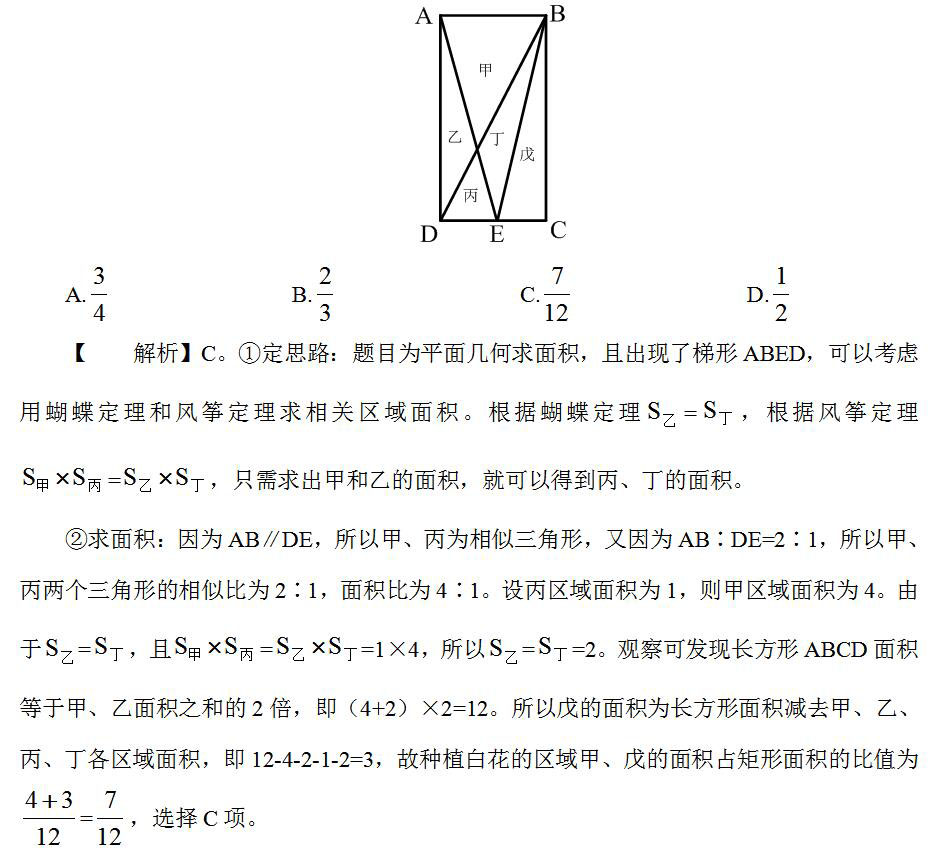

遇到平行四边形或者梯形被其对角线分成四个三角形区域,求各区域面积时,可以利用蝴蝶定理和风筝定理快速定思路、求面积。看到这里,相信备考的小伙伴,蝴蝶和风筝两招也已练成,快去求面积吧!




